圆的面积:几何之美,无限之境
一、圆的面积定义
圆的面积,是指圆形平面内所有点到圆心的距离之和所围成的平面图形的大小。它是一个几何学中的基本概念,也是计算圆形相关问题时不可或缺的参数。
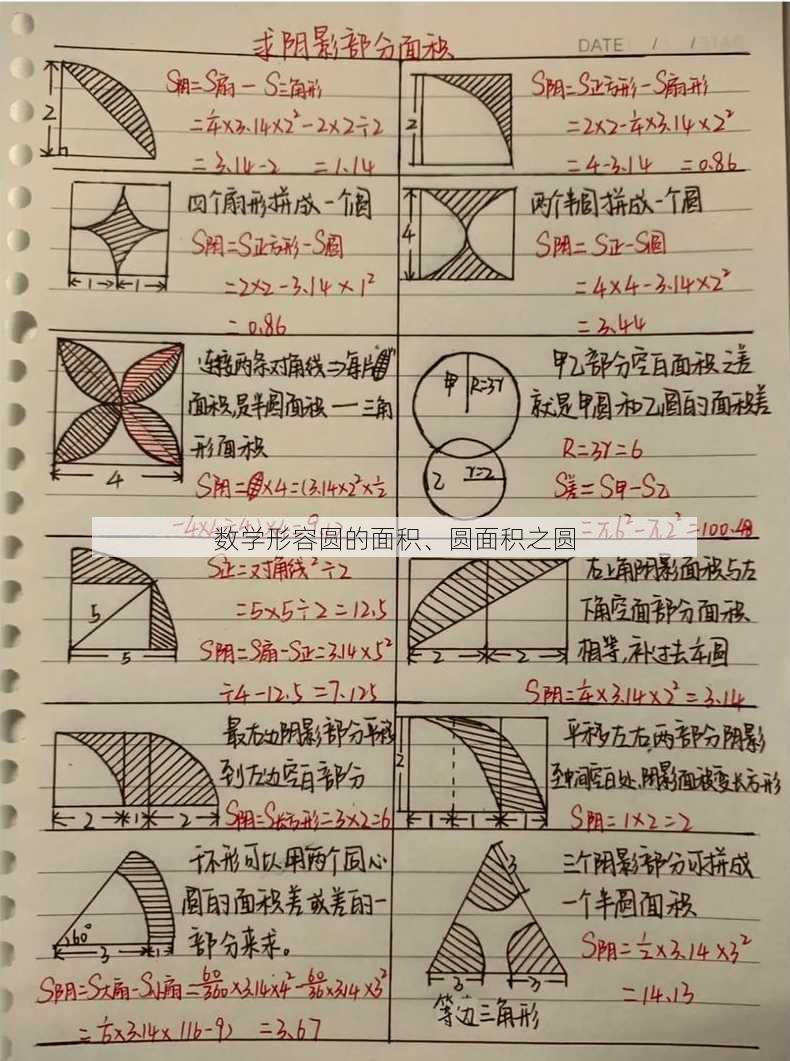
二、圆面积的计算公式
圆的面积可以通过以下公式计算得出:
[ A pi r^2 ]
其中,( A ) 代表圆的面积,( r ) 代表圆的半径,( pi ) 是一个常数,约等于 3.14159。
三、圆面积的应用
圆的面积在日常生活和工程应用中有着广泛的应用,以下是一些例子:
建筑设计:在建筑设计中,计算圆面积对于确定屋顶、门和窗户的大小至关重要。
农业:在农业中,圆面积的测量可以帮助农民精确计算田地面积,从而合理规划作物种植。
制造业:在制造业中,圆面积的计算对于确定零件尺寸和形状非常有用。
四、圆面积之圆
“圆面积之圆”可能是指一个特殊的圆,其面积与另一个圆的面积相等。这种情况在数学问题中可能涉及到圆的相似性或等面积问题。
五、情感与内涵
圆,作为一个完美的几何形状,象征着和谐、完美和无限。圆的面积计算,不仅是一种数学技能的体现,更是一种对生活美的追求和感悟。
相关问题的答案
问题一:圆的面积公式中的π是如何得来的?
π是一个无理数,其值无法精确表示为分数,但可以通过圆的周长与直径的比例来近似计算。
π可以通过几何方法,如割圆术,得到一个近似值。
π的精确值是通过计算机算法计算得出的,目前已知的最精确值为小数点后数十亿位。
问题二:圆的面积在实际生活中有哪些应用?
在家居装修中,计算天花板或地板的面积。
在汽车设计中,计算车轮的面积以优化轮胎设计。
在天文学中,计算太阳或行星的表面积。
问题三:如何理解“圆面积之圆”的概念?
“圆面积之圆”可能指的是两个圆,它们的面积相等。
这个概念可能出现在数学证明或几何问题中,要求找到与已知圆面积相等的另一个圆。
在实际应用中,这可能涉及到设计或工程问题,需要找到一个特定面积的圆形结构。
